Big O notation

Normally you would develop against a test-database. It probably contains about 10 people so you can do your programming and testing.. Once it’s done and QA’d, it will go live and people start to visit the site. After a year or so,.. the site is too slow. Adding more db servers is of no use, your system administrator is spending his holiday inside the my.cnf’s and after dumping a gazzilion GB’s of extra memory to the systems doesn’t help at all…  Sounds like it’s the code that’s falling behind.. it cannot cope sorting or handling user lists of 40.000 people, or arrays with more than a million items and even simple validation functions are way to slow.. why? what just happened?

Most PHP developers have never heard of Big-O, yet in web development big-O is maybe more important than any other aspect of development (ok, except for systems and OS programming maybe :) ). Centralized code can be executed by only 10 users a day, but the same code could quite possibly be run thousands of times per minute.

What is big O?

Big-O, or the landau notation is a mathematical principle that defines how well a function scales in respect to it’s arguments. To put it in plain English: big-O tells you how the relation in time between a strpos() function with a 10-char long string argument and a 1000000-char long string argument. It won’t tell you the specific times, but more the ratio between them on how many times faster or slower it is.

So, what’s the deal you might ask?

A lot…

Suppose you have a function that would sort data in array on certain conditions.. For instance, on alphabetical order by last name. Everybody can image that sorting 10 users would be a lot quicker than sorting 10 million users.. But how much quicker or better yet: how much longer would the latter take? When knowing the answer to this question, you KNOW how fast your code will be with a lot of users. You will know what the first bottleneck will be.. your code or the hardware. In other words, you just became aware of scalability.

Example 1:

Suppose you have a function called IsEven():

function isEven ($iNumber) {
  return ( ($iNumber & 1) == 0);
}

This function will check if a number is even, and if so, returns boolean true, otherwise it will return boolean false. For this function it does not matter if $iNumber is int(1), or int(100000005). If will always take the same amount of time for the function to do the check and return.

Now suppose we have written the function this way:

function isEven ($iNumber) {
  $bEven = true;
  for ($i=0; $i!=abs($iNumber); $i++) {
    if ($bEven == true) {
      $bEven = false;
    } else {
      $bEven = true;
    }
  }
  return $bEven;
}

Granted, it doesn’t make much sense to check it this way.. but I occasionally see code where the wrong algorithms are used so this example will suffice to make my point.

When we do a isEven(1), the for-loop will only be called once. It’s fast enough so no problems there. However, when we want to check the number 1000000 we might run into a wee bit of trouble since the function has to loop 1000000 times.

If we would put the first example function into a graph, where the X axis is $iNumber (ranging from 1 to 1000) and the time spend in the function on the Y axis, we would get a graph with a straight horizontal line. This would indicate that it doesn’t matter what number is given to the function, it always returns in the same time. This is called O(1), which is the most optimized function. It will always run in the same time no matter what you feed it. It’s a scalability dream come true so to speak :)

Now.. let’s analyze the second function. If we would plot $iNumber against time, we would see a straight line going up. This is more or less a straight line and will be O(N) (where N stands for the number of arguments or argument). The number of arguments is in direct relation with the time.

Example 2:

function getModuleInfoByID ($iModuleID) {
  foreach ($this->_aModuleInfo as $aInfo)  {
    if ($aInfo['id'] == $iModuleID) return $aInfo;
  }
  return null;
}

This method will return the module information of a specified ID or it will return null when the ID is not found. It is a very common way to find data by browsing over an array and return the correct one when found. Functions like these would be O(n) where N stands for the number of moduleInfo’s we have in our $_aModuleInfo property.

How could we optimize a function like this?

It would be nice to get rid of the iteration. Those pesky things are always a good way of throwing your code way down the O-line :) In order to do that, we have to change some other things as well.. For instance,.. if we made $_aModuleInfo into a associative array with the ID as key, we would suffice with a function like this:

function getModuleInfoByID ($iModuleID) {
  if (isset ($this->_aModuleInfo[$iModuleID])) return $this->_aModuleInfo[$iModuleID];
  return null;
}

at this point, we don’t care how long our $_aModuleInfo array is. It would not need to iterate over anything anymore and it doesn’t matter if we got 1 moduleInfo item, or 1 million.

However, there are some catches:

• what is the behavior of the isset()? Is it O(1) or maybe O(n) or even worse? You have to find that out as well which means you need to time your functions (and calls in those functions).
• You are only checking  on PHP-level. It could be a whole different ballgame on CPU-level. For instance: numeric arrays should be a lot faster than associative arrays (since they don’t involve a lookup of the hash). However, there is no real difference in time between an numeric and associative array in PHP.

The different O’s

There are too many and they are too complex :) Just stick with the basic few and see to which one your function behaves.. You probably never need an exact formula but as long as you know that your function is more behaving like O(log N) instead of O(N), you know enough..

A list of O-functions, ranging from the best to the worst:

• O(1)
  Constant time.. Arguments do not matter and the function duration stays always the same.

• O(log N)
  Logaritmic time..  The function time will increase rapidly in the beginning, but after a while they don’t have much impact. These are good when you know you always have a lot of items (like sorting users, articles, comments etc).

• O(n) Linear.
  The number of arguments is in direct relation with the time. Twice the number of arguments means twice the duration of the function.

• O(n^2)  Quadratic.
  Most of the time it means 2 iterations of the same dataset (like many unoptimized sorts algorithms).

• O(n^3) Cubic.
  The same as quadratic, but with one more extra loop. Recipe for disaster to happen :).

• O(n!) Factorial.
  These graphs go practically straight up. (for instance, faculty of 10 = 3628800, which means a lot of iterations). If you have functionality that behaves this way, really think about rewriting them since they will be very, very slow in a very short time.

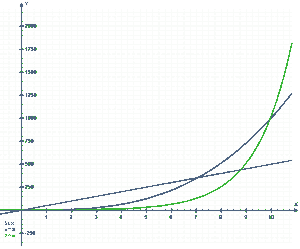
From http://nl.wikipedia.org/wiki/Bestand:Exponential.png, the red line is linear O(n), the blue one cubic O(n^3) and the green one exponential O(2^n). Note that even though the green once stays the best one until 8 items, after 10 items it is the worst.

When fetching data, we statistically have to search only half the array. To find a random number between 0 and 100, there is a 50% change that it will be lower than, and 50% change it will be higher (or equal) than 50.  However, big-O will define the worst case scenario. So searching sequentially trough an N-array will be O(N), not O(N/2).

Big-O Catches

Note that an O-notation does not say anything about speed itself. It only tells you about speed relative to the arguments. For example, in some situations, a O(n) function could be faster then a O(log n) or even a O(1) function. However, there will be a break-even point in where the other functions will be faster. It’s a trade-off you have to make between function and algorithm complexity and speed.

Time your functionality.. time it again and again and see the results.. they might not be as bad as you think (or maybe they are even worse  ;)). Code speaks for itself, but without timing you just don’t know :)

Conclusion

Know your functions and know how they behave. But always make sure you don’t over-optimize things.. making everything O(1) is a nice goal but realistically can never be done and there will always be a trade off between development time/budget and speed/optimization.